Natural Fermat's Spirals
Fermat's spiral is also known as a parabolic spiral. It's given by the polar equation r = k a^1/2 where r is the distance from the origin, k is a constant that determines how tightly wound the spiral is, and a is the polar angle. This type of spiral has the property of enclosing equal areas with every turn as it is illustrated below: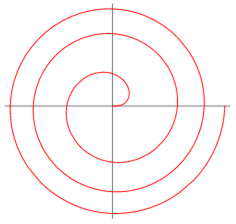
What do you know? Here is one such natural spiral. It's a tendril from my Antigone vine, ready to unfurl and hook onto whatever support it can find to climb. The amazing thing for this natural spiral is that it does not start from the origin, but from the stem of the vine. I think that this is an excellent way to efficiently search for a contact in three dimension with a minimum amount of tendril length.


1 comment:
Very interesting post and great shot!
Post a Comment